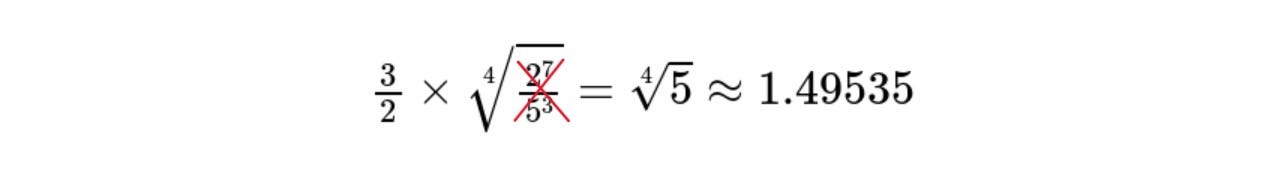Errata

Correction to a correction

The subscriber email that was sent out earlier this week for the latest post Throw a Temper, Pitch a Fit contained an error. In it, I presented an equation for calculating the size of fifths in quarter comma meantone, and a very shrewd 10-year-old brought to my attention that the math was wrong. The website has since been updated but unfortunately the original emails cannot be edited. I sincerely apologize for the confusion this may have caused.

Here is the old version with the mistake:

Here is the correct equation:

\(\frac{3}{2}\div\sqrt[4]{\frac{3^4}{5\cdot2^4}}=\frac{3}{2}\times\sqrt[4]{\frac{80}{81}}={\sqrt[4]{5}}\approx 1.49535\)

Vigilant readers may have noticed that instead of a syntonic comma, what I mistakenly put in the original email was actually the lesser diesis (a.k.a. enharmonic comma).

As we know, if all fifth in the circle of fifths are pure, the circle does not close, as 12 fifths come just a bit wider than seven octaves. Any temperament in tuning is essentially a way to close the circle by making certain compromises. In Pythagorean tuning, one of the fifths is narrowed. The size discrepancy between this out of tune “wolf interval” and the pure fifth is the Pythagorean comma:

\(\frac{(\frac{3}{2})^{12}}{2^7}=\frac{3^{12}}{2^{19}}\)

This is approximately 23.5 cents.

From the circle of fifth, we see that four stacked fifths gives us a third (plus two octaves). If both fifths and thirds are kept pure, the ends don’t quite meet. In quarter comma meantone, fifths are compromised in favor of pure thirds. The adjustment needed to apply to the fifths in order to keep the thirds pure is the syntonic comma:

\(\frac{(\frac{3}{2})^4}{\frac{5}{4}\cdot2^2}=\frac{3^4}{5\cdot2^4}=\frac{81}{80}\)

The syntonic comma is spread evenly among the stack of four fifths that makes a third, hence the name “quarter comma”. It is about 21.5 cents.

The quarter comma is an overcorrection in closing the circle of fifths. When all fifths are narrowed by a quarter comma, a gap is left. This gap is the lesser diesis:

\(\frac{2^7}{{(\frac{3}{2}}\cdot\sqrt[4]\frac{80}{81})^{12}}=\frac{2^7}{5^3}\)

Because the lesser diesis is added to one of the 12 fifths, unlike the narrow wolf in Pythagorean tuning, the wolf interval in quarter comma meantone is too wide, by about 41.1 cents.

Notice that the denominator on the right-hand side is the same thing as a pure-third-plus-two-octaves repeated three times:

\((\frac{5}{4}\cdot2^2)^3=5^3\)

So we could think of quarter comma meantone as a product of the “circle of thirds”. But of course, since a third has 4 semitones and an octave 12, and 4 and 12 are not coprime, we do not generate the whole chromatic scale this way, hence why we still need to tweak the fifths to make everything fit.

Tying everything together, three syntonic commas (because there are three stacks of four fifths in a circle of fifth) less a lesser diesis is equivalent to a Pythagorean comma. To check:

\({(\frac{3^4}{5\cdot2^4})^3}\div{\frac{2^7}{5^3}}=\frac{3^{12}}{2^{19}}\)

I hope this helps clear up some of the confusions caused by the previous mistake. Please excuse the formatting as the Substack LaTex editor is a little finicky. Please reach out if you spot any future issues, and make sure to always check the website for the latest updates.

Thank you for reading.